Wielu speedcuberów zastanawia się, jaka jest na coś szansa: na skipa, na łatwy scramble itd. Nie każdy potrafi to policzyć, a znalezienie poprawnej odpowiedzi bywa czasochłonne. W tym artykule pokażę, jak obliczyć szansę na otrzymanie LL skipa na kostce 3x3x3 w standardowej metodzie LBL lub CFOP.

Uwaga: uznajemy, że, jeśli do ułożenia kostki został tylko auf (ruch górną warstwą), to dostaliśmy LL skip. Dlatego można pominąć rozważania o liczbie różnych PLL-i z aufami po ich wykonaniu. W takim razie interesują nas tylko te sytuacje, w których najwięcej elementów jest dopasowanych do centrów - dzięki temu są one ułożone.

Oczywiście LL skip składa się z dwóch "mniejszych" skipów: OLL i PLL. Dlatego wystarczy obliczyć prawdopodobieństwo na oba te skipy (osobno), po czym pomnożyć je przez siebie - musimy otrzymać oba te skipy jednocześnie.

Najpierw zajmę się PLL skipem. Istnieją 22 PLL-e, w tym 1 to właśnie skip. Jednak ta liczba nie jest najbardziej istotna w kontekście obliczania prawdopodobieństwa - skipy (tak samo jak

) zdarzają się rzadziej od np. PLL Ja. Dlaczego tak się dzieje?

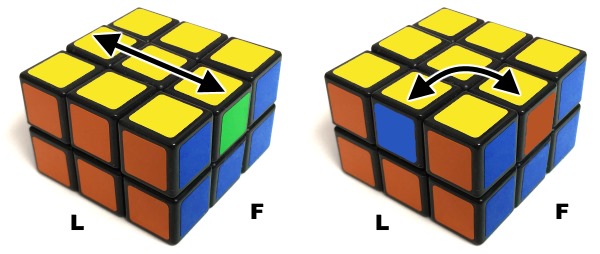
Oczywiście górną ścianę, na której spodziewamy się otrzymania PLL-a, "otaczają" 4 ściany. Powiedzmy, że górna ściana jest żółta, przednia jest czerwona, prawa jest zielona itd.. Rozważmy permutację Ua. Kiedy wykonamy tę permutację (na ułożonej kostce) z przodu, "pasek" złożony z trzech ułożonych elementów na górnej warstwie znajduje się z przodu (lub z tyłu - to zależy od wykorzystywanego algorytmu). Na drugiej kostce wykonajmy PLL Ua, mając żółtą ścianę z przodu. Następnie wróćmy do ustalonej orientacji (czerwony z przodu).

Okazuje się, że "paski" na obu kostkach znajdują się w innych miejscach. A to znaczy, że to są inne sytuacje - inne krawędzie są nieułożone. Dlatego liczymy te sytuacje nie jako 1 PLL, ale jako 2 różne układy elementów. Oczywiście, kiedy podobny eksperyment wykonamy z dwóch pozostałych orientacji (biała lub pomarańczowa ściana z przodu), otrzymamy podobne wyniki. Dlatego permutacja Ua odpowiada aż 4 układom elementów.

Teraz rozważmy permutację H. Zróbmy podobnie: wykonajmy ją w 2 różnych orientacjach. Okazuje się, że na obu kostkach sytuacja jest taka sama - permutacja H odpowiada tylko jednemu układowi elementów.

Dlaczego jednemu PLL-owi przypisujemy 4, a innemu - 1 układ?

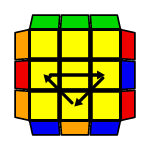
PLL-e często przedstawiane są na rysunkach w formie strzałek łączących elementy, które zamieniają algorytmy przypisane danym permutacjom. Ich zwroty oznaczają, w jakiej kolejności zamieniają się elementy - np. PLL Ua ma strzałki o zwrotach przeciwnych do PLL Ub. Ale w PLL-ach, w których 2 elementy zamieniają się ze sobą, strzałki o przeciwnych zwrotach nałożone są na siebie, tworząc "podwójną strzałkę".

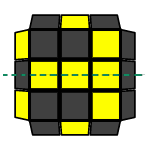
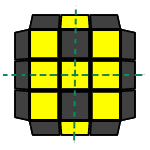
Permutacja H ma dwie takie podwójne strzałki tworzące kształt "+". Zauważmy, że taki układ ma 4 osie symetrii: 2 ukośne, 1 poziomą i 1 pionową (zaznaczyłem je na rysunkach kolorem zielonym). To znaczy, że strzałki po jednej stronie osi tworzą odbicie lustrzane strzałek po drugiej stronie. Taka reprezentacja pokazuje dokładnie to, co zaobserwowaliśmy wcześniej - jeżeli wykonamy PLL H z jakiejkolwiek orientacji, to ten układ będzie symetryczny do tego, który można wykonać z innej orientacji, więc te układy są takie same.

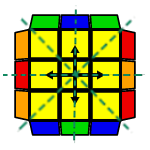
Natomiast permutacja Ua reprezentowana jest przez 3 strzałki z których żadna nie jest podwójna - nie można znaleźć żadnej osi symetrii (nawet, gdy wydaje się, że taka istnieje, okazuje się, że po "odbiciu" strzałki mają przeciwne zwroty, a więc tworzą permutację Ub, która oczywiście jest innym PLL-em). To oznacza, że żadne układy się nie pokrywają, a więc wszystkie 4 są różne.

Właśnie wykazałem, że na permutację Ua można trafić 4 razy częściej niż na permutację H. Jak jest z innymi PLL-ami? Np. wszystkie permutacje G tworzą po 4 układy (0 osi symetrii, bo strzałki nie są podwójne), a permutacja E tworzy 2 układy (2 osie symetrii - prostopadła i równoległa). Permutacja T ma tylko jedną oś symetrii, co odpowiada 4 różnym układom elementów.

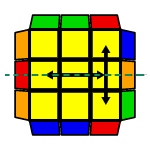
Łatwo zauważyć, że prawie wszystkie PLL-e, które zamieniają 2 krawędzie i 2 narożniki, mają maksymalnie 1 oś symetrii do kierunku podwójnych strzałek), co odpowiada 4 układom. Wyjątkiem są permutacje Na i Nb, których działanie jest trochę trudniejsze do zrozumienia (można ustawić strzałki na 2 różne sposoby) - ważne jest to, że odpowiadają w sumie tylko 2 układom. Kiedy pojawia się 3-cykl, strzałki nie są podwójne, więc PLL-e odpowiadają 3 układom. 2 osie symetrii - 2 układy, 4 - 1 układ. Skip to także 1 układ.

Po podzieleniu liczby układów odpowiadającym skipowi przez sumę wszystkich układów dostajemy szansę na otrzymanie PLL skipa - 1/72.

Z OLL-ami należy zrobić to samo - obliczyć liczbę osi symetrii figur, które tworzą zorientowane elementy (tutaj analogia ze strzałkami raczej nie pomoże). Np. oba OLL-e T mają 1 oś symetrii, co odpowiada 4 układom, ale OLL H ma już 2 osie symetrii - 2 układy. Tylko 2 OLL-om (skipowi i OLL-owi X) odpowiada 1 układ. Po zliczeniu wszystkich przypadków dostajemy szansę 1/216 na wystąpienie OLL skipa.

Zauważ, że istnieją algorytmy, które tylko orientują elementy - nie zamieniają żadnych elementów miejscami, więc każdemu OLL-owi odpowiadają 72 sytuacje tożsame PLL-owi. W takim razie wystarczy pomnożyć prawdopodobieństwo uzyskania OLL skipa przez szansę na otrzymanie PLL skipa:

1/72*1/216 = 1/15552

Gdybyśmy chcieli odrzucić sytuacje, w których do ułożenia zostaje auf, wystarczy podzielić tę liczbę przez 4.

Zadanie dla czytelnika: jaka jest szansa na LL skipa na kostce 3x3x2? Inaczej mówiąc, jaka jest szansa na otrzymanie PLL skipa na układance, na której nie ma ograniczenia dotyczącego parity - na 3x3x2 można otrzymać sytuację, w której zamienione są np. 2 krawędzie i nic więcej.